Plug-and-Play: Algorithms, Parameters Tuning and Interpretation
Plug-and-Play: 算法的推导, 利用强化学习选择参数与证明收敛性的两种框架
本文为北京大学最优化讨论班 2022 年 3 月 1 日的讲稿
- https://ieeexplore.ieee.org/document/8962388?arnumber=8962388
(IEEE Signal Processing Magzine) - https://proceedings.mlr.press/v119/wei20b
(ICML 2020 Award Paper) - https://jmlr.org/papers/v23/20-1297.html
(JMLR) - https://epubs.siam.org/doi/abs/10.1137/20M1337168
(SIAM Journal on Imaging Sciences) - https://epubs.siam.org/doi/10.1137/16M1102884
(SIAM Journal on Imaging Sciences)
等几篇文章的主要内容, 着重介绍它们在理论上的进展及各方法提供的 insights.
maximum a posteriori probability (MAP) estimate
考虑如下的线性反问题:
\[y=Ax+\varepsilon.\]给定带有噪音 \(\varepsilon\) 的观测值 \(y\), 我们需要从中恢复出原始信号 \(x\). 这一类问题广泛出现在图像处理领域. 在贝叶斯统计中, 常将这类问题建模为最大化后验概率 (Maximum A Posteriori) 估计. 根据贝叶斯公式, 观测值为 \(y\) 时原信号为 \(x\) 的后验概率满足
\[\mathbb{P}(x\mid y)=\frac{\mathbb{P}(y\mid x)\mathbb{P}(x)}{\mathbb{P}(y)}.\]最大化后验概率估计试图从所有可能的 \(x\) 中选出使得后验概率 \(\mathbb{P}(x\mid y)\) 最大的那个. 注意到, 上式的分母仅被 \(y\) 决定, 最大化 \(\mathbb{P}(x\mid y)\) 等价与最大化分子 \(\mathbb{P}(y\mid x)\mathbb{P}(x)\). 涉及两函数之积的优化往往较为复杂, 而概率的特性决定了 \(\mathbb{P}(y\mid x)>0\) 与 \(\mathbb{P}(x)>0\) 在大多数情形下成立. 因此, 我们可以引入对数, 将乘积转换为求和, 此时最大化后验概率估计等价于
\[\min_{x}\, -\ln\mathbb{P}(y\mid x) - \ln\mathbb{P}(x).\]在实践中, 加性白高斯噪声 (Additive White Gaussian Noise) 是一种被广泛采用的假设. 在这一假设下, 噪声 \(\varepsilon\sim \mathcal{N}(0,\sigma^2I)\), 其中 \(\mathcal{N}(0,\sigma^2I)\) 是均值为 \(0\), 协方差矩阵为 \(\sigma^2I\) 的多元高斯分布. 于是
\[\mathbb{P}(y\mid x)=\mathbb{P}(\varepsilon=y-Ax)=\frac{1}{(2\pi\sigma^2)^{n/2}}\exp\left(-\frac{\Vert Ax-y\Vert ^2}{2\sigma^2}\right).\]忽略常数后, 最大化后验概率在加性白高斯噪声的假设下等价于
\[\min_{x}\, \frac{1}{2\sigma^2} \Vert Ax-y\Vert ^2 - \ln\mathbb{P}(x).\]此时, 只要选定先验概率 \(\mathbb{P}(x)\) 即可给出优化模型. 我们将 \(- \ln\mathbb{P}(x)\) 记为 \(\varphi(x)\), 则 \(\varphi(x)\) 应当尽可能与某个函数的负对数相等, 同时使得上述优化问题易于处理. 一种常见的选择是 \(\varphi(x)=\lambda\Vert \Psi x\Vert _1\), 且 \(\Psi^\top\Psi=I\), \(\lambda>0\). 这样的 \(\varphi(x)\) 在保证优化问题凸性的同时使得输出 \(\Psi x\) 较为稀疏. \(\varphi(x)\) 常被称作正则项, 它向模型中添加了某种先验信息, 有大量的工作致力于选取合适的 \(\varphi(x)\).
去噪问题
当线性反问题中的 \(A\) 是单位矩阵 \(I\) 时, 观测值与原信号满足 \(y=x+\varepsilon\). 这种特殊的线性反问题被称为去噪, 在去噪问题上表现最好的工作都是基于物理直觉设计算法或运用神经网络. 我们能否借助去噪问题的算法来处理一般的线性反问题呢? 答案是肯定的, 这正是 Plug-and-Play 的做法.
ADMM
在正式介绍 Plug-and-Play 前, 我们先来看如何处理最大化后验概率估计:
\[\min_{x}\, \frac{1}{2\sigma^2} \Vert Ax-y\Vert ^2 + \varphi(x).\]直接针对 \(x\) 进行优化往往困难重重, 我们可以引入辅助变量 \(v\), 将上述问题等价转化为约束优化问题
\[\min_{x}\, \frac{1}{2\sigma^2} \Vert Ax-y\Vert ^2 + \varphi(v), \quad \text{ s.t. } x=v.\]Alternating Direction Method of Multipliers (ADMM) 非常适合用来求解这种变量分块的问题. 引入乘子 \(z\) 与罚因子 \(1/\eta\), 其增广拉格朗日函数为
\[\begin{aligned} L(x,v;u)&=\frac{1}{2\sigma^2} \Vert Ax-y\Vert ^2 + \varphi(v)-z^\top(x-v) + \frac{1}{2\eta}\Vert x-v\Vert ^2\\ &=\frac{1}{2\sigma^2} \Vert Ax-y\Vert ^2 + \varphi(v) + \frac{1}{2\eta}\Vert x-v-u\Vert ^2-\frac{1}{2\eta}\Vert u\Vert ^2.\quad(u=\eta z) \end{aligned}\]于是 ADMM 所给出的迭代为
\[\left\{ \begin{aligned} x^{k+1}&=\underset{x}{\arg\min}\, L(x,v^k;u^k)=(A^\top A+\frac{\sigma^2}{\eta}I)^{-1}\left(A^\top y+\frac{\sigma^2}{\eta}(v^k-u^k)\right),\\ v^{k+1}&=\underset{v}{\arg\min}\, L(x^{k+1},v;u^k)=\operatorname{prox}_{\eta\varphi(\cdot)}(x^{k+1}-u^k),\\ u^{k+1}&=u^k-(x^{k+1}-v^{k+1}). \end{aligned}\right.\]PnP-ADMM
注意到 proximal 算子
\[\begin{aligned} \operatorname{prox}_{\eta\varphi(\cdot)}(x^{k+1}-u^k) &= \underset{v}{\arg\min}\, \eta\varphi(v)+\frac{1}{2}\Vert v-x^{k+1}+u^k\Vert ^2\\ &=\underset{v}{\arg\min}\, \varphi(v)+\frac{1}{2\eta}\Vert v-x^{k+1}+u^k\Vert ^2 \end{aligned}\]可以被视为观测值为 \(x^{k+1}-u^k\), 正则项为 \(\varphi(v)\), 噪声服从 \(\mathcal{N}(0,\eta I)\) 的去噪问题所对应的最大化后验概率估计! 基于这种形式上的相似性, 我们考虑用现有的去噪算法替代 ADMM 中对 \(v\)-子问题的优化. 将去噪算法抽象为 \(f(\cdot,\eta)\), 保留 \(\eta\) 是因为去噪算法中常常需要指定噪声的大小. 于是 PnP-ADMM 写作
\[\left\{ \begin{aligned} x^{k+1}&=(A^\top A+\frac{\sigma^2}{\eta}I)^{-1}\left(A^\top y+\frac{\sigma^2}{\eta}(v^k-u^k)\right),\\ v^{k+1}&=f(x^{k+1}-u^k,\eta),\\ u^{k+1}&=u^k-(x^{k+1}-v^{k+1}). \end{aligned}\right.\]令人惊喜的是, 这样一种简单的替换就可以带来巨大的提升. 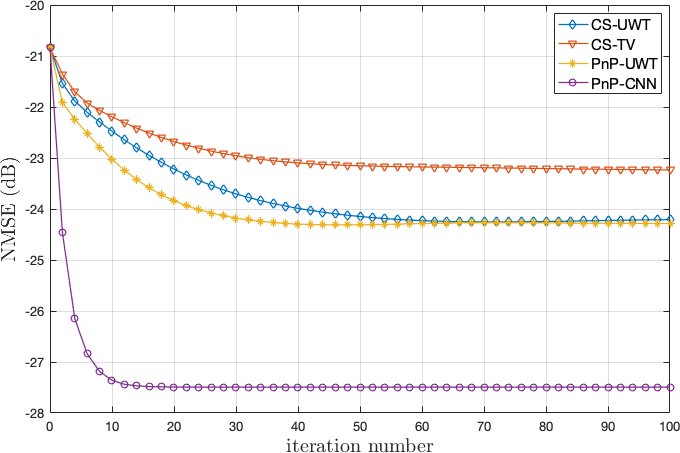
前缀 CS 是 Compress Sensing 的缩写, 是一种传统方法, 纵坐标 NMSE 全称 Normalized Mean-Squared Error, 度量了算法所恢复出的信号与真实的原始信号的差距, UWT 是 undecimated wavelet transform 的缩写. TV 表示 Total Variation, CNN 则表示用基于卷积神经网络的去噪算法替换 v-迭代所得到的 PnP 算法. 可以看出, 基于 PnP 的方法在收敛速度与解的质量上都优于传统算法.
参数的选择
细心的同学可能已经注意到了在 PnP-ADMM 中, 参数 \(\eta\) 的取值是固定的. 正如传统的 ADMM 算法中, 罚因子的选择会影响算法的效果, 在 PnP-ADMM, 不同的 \(\eta\) 表现也大不相同. 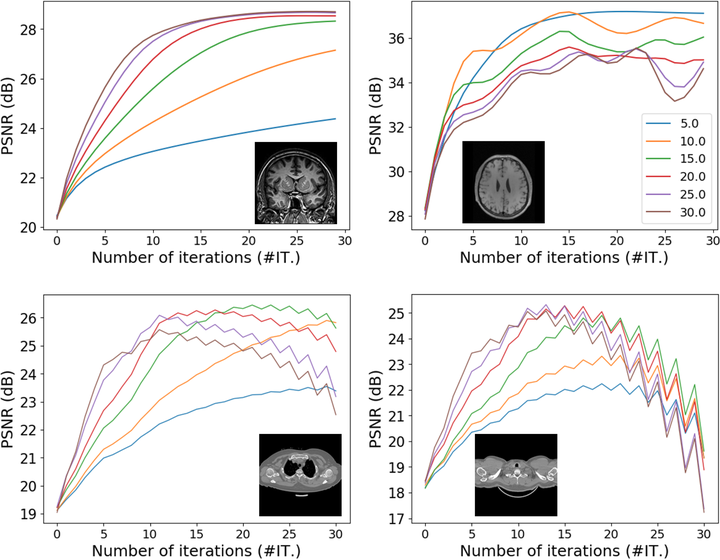
纵坐标为 PSNR (Peak Signal-to-Noise Ratio) 峰值信噪比, 其度量了图像恢复的质量, 不同颜色表示 eta 取不同值时 PSNR 随迭代次数变化的曲线.
PSNR计算方法为 (参考 https://zhuanlan.zhihu.com/p/50757421):
给定一个大小为 \(m \times n\) 的干净图像 \(I\) 和噪声图像 \(K\), 均方误差 (MSE) 定义为:
\[\text{MSE}=\frac{1}{m n} \sum_{i=0}^{m-1} \sum_{j=0}^{n-1}[I(i, j)-K(i, j)]^{2}\]PSNR(dB) 定义为:
\[\text{PSNR}=10\log _{10}\left(\frac{\text{MAX}_{I}^{2}}{\text{MSE}}\right)\]其中 \(\text{MAX}_{I}^{2}\) 为图片可能的最大像素值. 如果每个像素都由 8 位二进制来表示, 那么就为 255. 如果像素值由 B 位二进制来表示, 那么 \(\text{MAX}_{I}=2^{B}-1\).
这说明噪声水平的选择对 PnP-ADMM 的影响同样巨大, 针对不同的图片, 最优的噪声水平也是不同的. 受此启发, 我们联想到在 ADMM 中常根据原始残差与对偶残差的相对大小来动态调整罚因子, 以加速收敛. 因此, 我们可以将 PnP-ADMM 中的 \(\eta\) 与 \(\sigma^2/\eta\) 变为随步数动态调整的参数 \(\eta_k\), \(\mu_k\). 但问题在于 PnP-ADMM 并不是从某个优化问题基于 ADMM 导出的迭代格式, ADMM 中的理论可能失效, 此时该如何选取动态的步长 \(\eta_k\), \(\mu_k\) 呢?
Markov Decision Process
实际上, 若从更加抽象的角度来考察迭代算法, 它们都可以被看作一种特殊的马尔可夫决策过程. 具体而言, 我们将 \(x^k\), \(v^k\), \(u^k\) 视为 Agent 在时刻 \(k\) 的状态 (State) \(s_k\). 将两个参数 \(\eta_k\), \(\mu_k\) 看作 Agent 在时刻 \(k\) 采取的动作 (Action), 同时 Agent 还需决定是否终止迭代, 这可以通过一个二元变量 \(\tau_k\) 来表达, 将这些随 \(k\) 变化的参数记为 \(a_k\). 那么其 \(k+1\) 的状态 \(s_{k+1}\) 就被 \(s_k\) 与 \(a_k\) 决定, 用 MDP 的术语来说, \(s_{t+1}=p(s_t,a_t)\), 其中 \(p(s_t,a_t)\) 是概率转移函数, 在这种设定下等价于策略 (Policy). 最后, 我们基于 PnP-ADMM 希望在尽可能少的步数内提升信号恢复质量的目标定义奖励函数 (Reward)
\[r\left(s_{t}, a_{t}\right)=\left[\zeta\left(p\left(s_{t}, a_{t}\right)\right)-\zeta\left(s_{t}\right)\right]-\eta.\]其中 \(\zeta(s_t)\) 是第 \(t\) 步恢复出的信号的 PSNR 值, 而 \(\eta\) 则是一个常数, 用来惩罚 PnP-ADMM 在第 \(t\) 步仍未结束迭代.
将以上论述归纳为标准的 MDP, 则得到四元组 \((\mathcal{S}, \mathcal{A}, p, r)\).
- \(\mathcal{S}\): 状态空间, 任何可行的 \(x^k\), \(v^k\), \(u^k\) 三元组.
- \(\mathcal{A}\): 动作空间, 任何可行的 \(\eta_k\), \(\mu_k\) 二元组与 \(\tau_k\in\{0,1\}.\)
- \(p\): 概率转移函数, PnP-ADMM 在给定 \(a_t\), \(s_t\) 后的一步迭代.
- \(r\): 奖励函数, \(r\left(s_{t}, a_{t}\right)=\left[\zeta\left(p\left(s_{t}, a_{t}\right)\right)-\zeta\left(s_{t}\right)\right]-\eta.\)
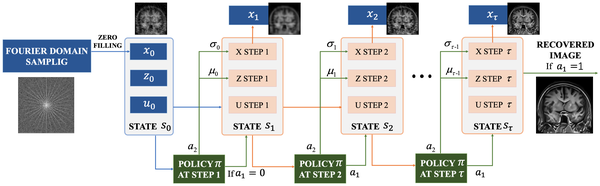
将 PnP-ADMM 建模为强化学习的示意图.
有了这种建模, 剩下的工作就是精确刻画其训练过程. 给定轨迹 (Trajectory)
\[T=\left\{s_{0}, a_{0}, r_{0}, \cdots, s_{N}, a_{N}, r_{N}\right\}\]与折现因子 (Factor) \(\rho\), 在时刻 \(t\) 的回报 (Return) 定义为
\[R_{t}=\sum_{t^{\prime}=0}^{N-t} \rho^{t^{\prime}} r\left(s_{t+t^{\prime}}, a_{t+t^{\prime}}\right).\]而我们的目标则是得到一个策略 \(\pi\), 使得由该策略导出的轨迹在初始时刻回报的期望值最大
\[J(\pi)=\mathbb{E}_{s_{0}, \pi}\left[R_{0}\right],\quad \pi(a \mid s): \mathcal{S}\times \mathcal{A} \rightarrow [0,1].\]其状态值函数 (State-value function) 定义为
\[V^{\pi}(s)=\mathbb{E}_{\pi}\left[R_{0} \mid s_{0}=s\right].\]动作值函数 (Action-value function) 定义为
\[Q^{\pi}(s, a)=\mathbb{E}_{\pi}\left[R_{0} \mid s_{0}=s, a_{0}=a\right].\]而策略 \(\pi\) 则由两个子策略 \(\pi_1\), \(\pi_2\) 组成. 其中 \(\pi_1\) 是一个随机的策略, 以一定概率输出 \(0\), \(1\), 若输出为 \(1\) 则继续迭代, 否则终止迭代. 而 \(\pi_2\) 是一个确定性策略, 它本质上由 PnP-ADMM 的几步迭代组成, 是一个输出为连续空间的确定性策略.
Actor-critic Framework
策略的训练用到了著名的 Actor-critic Framework. 首先定义策略网络 (actor): \(\pi_\theta=(\pi_1,\pi_2)\), 其中 \(\theta = (\theta_1,\theta_2)\).
- \(\pi_1(\cdot\mid s)\): \(\mathcal{S}\times \{0,1\}\to [0,1]\), 由 \(\theta_1\) 控制.
- \(\pi_2(s)\): \(\mathcal{S}\to \mathcal{A}\), 由 \(\theta_2\) 控制.
再定义价值网络 (critic): \(V_{\phi}^{\pi}\left(s_{t}\right)\), 其中 \(\phi\) 是该网络的参数.
价值网络的训练目标是使其尽可能满足贝尔曼方程 (Bellman equation), 损失函数为
\[L_{\phi}=\mathbb{E}_{s \sim B, a \sim \pi_{\theta}(s)}\left[\frac{1}{2}\left(r(s, a)+\gamma V_{\hat{\phi}}^{\pi}(p(s, a))-V_{\phi}^{\pi}(s)\right)^{2}\right].\]\(\pi_1\) 与 \(\pi_2\) 的训练则使用了策略梯度法 (Policy Gradient). 采用免模型 (Model-free) 的方法来训练 \(\pi_1\), 其梯度为
\[\nabla_{\theta_{1}} J\left(\pi_{\theta}\right)=\mathbb{E}_{s \sim B, a \sim \pi_{\theta}(s)}\left[\nabla_{\theta_{1}} \log \pi_{1}\left(a_{1} \mid s\right) A^{\pi}(s, a)\right].\]而 \(\pi_2\) 的训练则是基于模型的, 其梯度为
\[\nabla_{\theta_{2}} J\left(\pi_{\theta}\right)=\mathbb{E}_{s \sim B, a \sim \pi_{\theta}(s)}\left[\nabla_{a_{2}} Q^{\pi}(s, a) \nabla_{\theta_{2}} \pi_{2}(s)\right].\]整个训练过程的伪代码摘录如下, 由于这部分并非我们关注的重点, 故较为简略, 请感兴趣的读者参阅原论文: https://jmlr.org/papers/v23/20-1297.html. 
训练过程的伪代码.
数值试验的结果表明, 通过强化学习得到的参数在恢复效果与迭代次数上都优于其他方法 (见下图中的 Ours 栏目, PSNR 的计算方法上文已给出, \(\#\mathrm{IT}.\) 表示迭代次数). 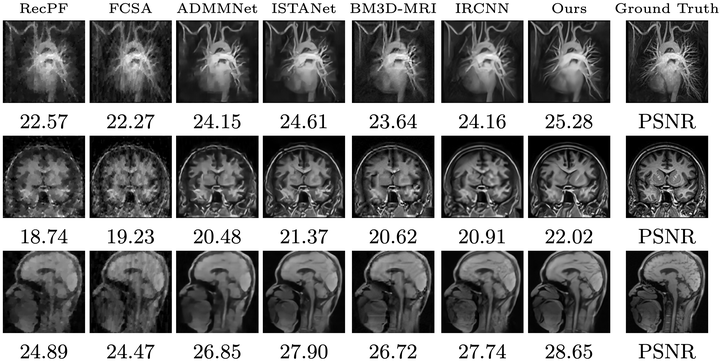
不同方法的恢复效果.
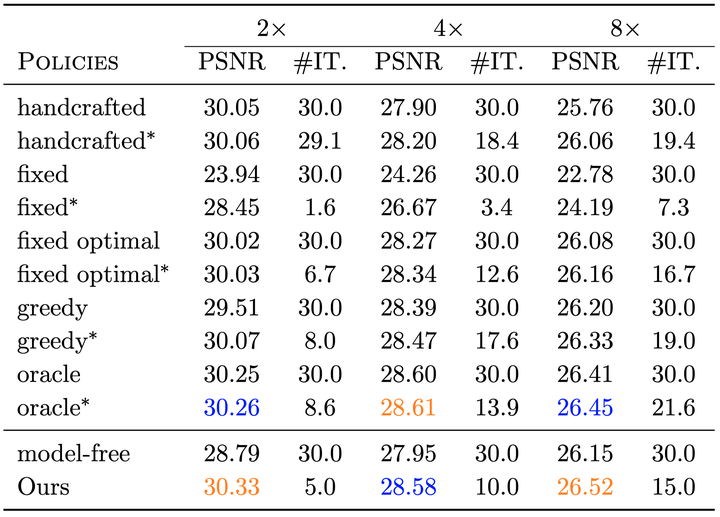
不同方法恢复效果与迭代次数的对比, IT 表示迭代次数.
对 PnP-ADMM 的再思考
在上文的推导中, 我们根据形式的相似性想到用去噪算法 \(f\) 替代 ADMM 中的 \(v\)-迭代, 但 \(f\) 很可能不是任何正则项 \(\varphi(\cdot)\) 所对应的 proximal 算子. 只有当
\[p({x})\propto \exp(-\varphi({x})),\quad {z}-{z}_{\mathrm{true}}\sim\mathcal{N}({0},\eta{I})\]时, \(f\) 才与 \(\operatorname{prox}_{\eta\varphi(\cdot)}({z})\) 一致. 然而 \(f\) 很可能不正比于 \(\exp(-\varphi({x}))\), 而
\[\left({x}_{k}+{u}_{k-1}\right)-\left({x}_{k}+{u}_{k-1}\right)_{\mathrm{true}}\]的分布也未知! 因此 PnP 只是根据形式上的相似性导出的结果. 那么能否从理论上去解释它呢? 既然 PnP-ADMM 并非某一优化问题所对应的 ADMM 算法, 那么它收敛吗? 如果收敛, 又收敛于什么值?
Regularization by Denoiser (RED)
为了回答上述问题, 我们先介绍 Regularization by Denoiser (RED) 方法, 这一方法在选择了适当的去噪算子与超参数后可以达到 SOTA 的表现, 同时, 基于这一方法可以给出 PnP-ADMM 的收敛性. RED 即利用去噪算子做正则项, 我们定义
\[\rho_{\operatorname{RED}}({x})\triangleq \frac{1}{2}\langle{x}, {x}-{f}({x})\rangle, \quad\ell({x} ; {y})=\frac{1}{2 \sigma^{2}}\Vert {y}-{A} {x}\Vert _2^2.\]则其所对应的 MAP 问题为
\[\widehat{\boldsymbol{x}}_{\mathrm{RED}}=\underset{\boldsymbol{x}\in \mathbb{R}^{n}}{\arg\min}\; \ell(\boldsymbol{x} ; \boldsymbol{y})+\rho_{\operatorname{RED}}(\boldsymbol{x}).\]神奇的是, 当 \(f\) 具有如下四个性质时
Local Homogeneity:
\[\boldsymbol{f}((1+\varepsilon) \boldsymbol{x})=(1+\varepsilon) \boldsymbol{f}(\boldsymbol{x}),\quad\forall \boldsymbol{x} \in \mathbb{R}^{n}, 0 < \varepsilon \ll 1.\]\(\boldsymbol{f}(\cdot)\) is differentiable where \(J \boldsymbol{f}\in \mathbb{R}^{n\times n}\) denotes its Jacobian.
Jacobian Symmetry: \(J \boldsymbol{f}(\boldsymbol{x})^\intercal=J \boldsymbol{f}(\boldsymbol{x}), \forall \boldsymbol{x} \in \mathbb{R}^{n}\).
The spectral radius the Jacobian satisfies \(\eta(J \boldsymbol{f}(\boldsymbol{x})) \leq 1\).
其最优化条件恰好为
\[{0}=\frac{1}{\sigma^{2}} {A}^{\intercal}({A} \widehat-{y})+\frac{1}{\eta}(\widehat-{f}(\widehat)).\]其证明如下 (开摆, 直接贴 slides 了)

RED 最优性条件的推导
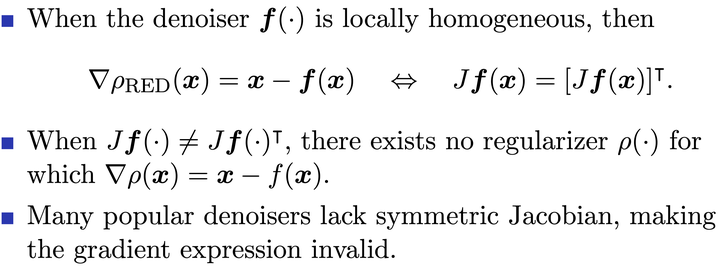
RED 的注记
那么这里介绍的 RED 和之前介绍的 PnP 有什么区别呢? 我们用一个 toy example 来进行说明. 考虑 \(\boldsymbol{f}(\boldsymbol{z})=\boldsymbol{W} \boldsymbol{z}\), 其中 \(\boldsymbol{W}=\boldsymbol{W}^{\top}\). \(\boldsymbol{f}\) 是 \(\varphi(\boldsymbol{x})=(1 / 2 \eta) \boldsymbol{x}^{\top}\left(\boldsymbol{W}^{-1}-\boldsymbol{I}\right) \boldsymbol{x}\) 所对应的 proximal 算子.
PnP 面临的优化问题为
\[\widehat{\boldsymbol{x}}_{\mathrm{pnp}}=\underset{\boldsymbol{x}}{\operatorname{argmin}}\left\{\frac{1}{2 \sigma^{2}}\Vert \boldsymbol{y}-\boldsymbol{A} \boldsymbol{x}\Vert ^{2}+\frac{1}{2 \eta} \boldsymbol{x}^{\top}\left(\boldsymbol{W}^{-1}-\boldsymbol{I}\right) \boldsymbol{x}\right\}.\]而 RED 则试图求解
\[\widehat{\boldsymbol{x}}_{\mathrm{red}}=\underset{\boldsymbol{x}}{\operatorname{argmin}}\left\{\frac{1}{2 \sigma^{2}}\Vert \boldsymbol{y}-\boldsymbol{A x}\Vert ^{2}+\frac{1}{2 \eta} \boldsymbol{x}^{\top}(\boldsymbol{I}-\boldsymbol{W}) \boldsymbol{x}\right\}.\]可以看出, 它们的区别在于正则项中对误差的 scale 不同, PnP 与 RED 相比正好差了一个 \(W\).
如何理解 RED: Score Matching
给定训练集 \(\{\boldsymbol{x}_t\}_{t=1}^{T}\), empirical prior model 定义为
\[\widehat{p}(\boldsymbol{x}) \triangleq \frac{1}{T} \sum_{t=1}^{T} \delta\left(\boldsymbol{x}-\boldsymbol{x}_{t}\right),\]其中 \(\delta\) 是狄拉克函数. 将狄拉克函数 \(\delta\left(\boldsymbol{x}-\boldsymbol{x}_{t}\right)\) 用协方差矩阵为 \(\eta I\) 均值为 \(x_t\) 的高斯分布 \(\mathcal{N}\left(\boldsymbol{x} ; \boldsymbol{x}_{t}, \eta \boldsymbol{I}\right)\) 替换则得到 kernel density estimation (KDE):
\[\tilde{p}(\boldsymbol{x} ; \eta) \triangleq \frac{1}{T} \sum_{t=1}^{T} \mathcal{N}\left(\boldsymbol{x} ; \boldsymbol{x}_{t}, \eta \boldsymbol{I}\right).\]将 \(\tilde{p}\) 视为 MAP 中对 \(x\) 的先验估计, 则 MAP 问题变为
\[\widehat{\boldsymbol{x}}=\underset{\boldsymbol{x}}{\operatorname{argmin}}\;\frac{1}{2 \sigma^{2}}\Vert \boldsymbol{y}-\boldsymbol{A x}\Vert ^{2}-\ln \tilde{p}(\boldsymbol{x} ; \eta).\]其最优化条件为
\[\mathbf{0}=\frac{1}{\sigma^{2}} \boldsymbol{A}^{\top}(\boldsymbol{A} \widehat{\boldsymbol{x}}-\boldsymbol{y})-\nabla \ln \tilde{p}(\widehat{\boldsymbol{x}} ; \eta)\]若将去噪算子选为最小均方误差 \(\boldsymbol{f}_{\mathrm{mmse}}(\boldsymbol{z};\eta)=\mathbb{E}[\boldsymbol{x}\mid\boldsymbol{z}]\), 其中 \(\boldsymbol{z}=\boldsymbol{x}+\mathcal{N}(\mathbf{0}, \eta \boldsymbol{I}), \boldsymbol{x} \sim \widehat{p}\). 则利用 Tweedie’s formula 可以得到
\[\nabla \ln \tilde{p}(\boldsymbol{z} ; \eta)=\frac{1}{\eta}\left(\boldsymbol{f}_{\mathrm{mmse}}(\boldsymbol{z} ; \eta)-\boldsymbol{z}\right).\]而上式恰好是 RED 在 \(f\) 为最小均方误差 \(\boldsymbol{f}_{\mathrm{mmse}}(\boldsymbol{z};\eta)=\mathbb{E}[\boldsymbol{x}\mid\boldsymbol{z}]\) 时的最优性条件, 这就从建模的角度给出 RED 的直觉. 但如果 \(f\) 不等于 \(\boldsymbol{f}_{\mathrm{mmse}}\) 呢, 此时又该如何理解 RED? 我们考虑一个由神经网络给出的去噪算子 \(f_\theta\), 其中 \(\theta\) 是参数, 训练策略为
\[\min_{\theta}\;\mathbb{E}\Vert \boldsymbol{x}-\boldsymbol{f}_{\theta}(\boldsymbol{z})\Vert ^2,\quad\text{where}\quad \boldsymbol{x}\sim \widehat{p},\quad \boldsymbol{z}=\boldsymbol{x}+\mathcal{N}(\mathbf{0}, \eta \boldsymbol{I}).\]利用最小均方误差 (MMSE) 所具备的正交性质 (类似于欧氏空间中的正交分解), 损失函数又可以分解为
\[\mathbb{E}\left\Vert \boldsymbol{x}-\boldsymbol{f}_{\boldsymbol{\theta}}(\boldsymbol{z})\right\Vert ^{2}= \mathbb{E}\left\Vert \boldsymbol{x}-\boldsymbol{f}_{\mathrm{mmse}}(z ; \eta)\right\Vert ^{2} +\mathbb{E}\left\Vert \boldsymbol{f}_{\mathrm{mmse}}(\boldsymbol{z} ; \eta)-\boldsymbol{f}_{\boldsymbol{\theta}}(\boldsymbol{z})\right\Vert ^{2}.\]再次使用 Tweedie’s formula, 我们得到
\[\begin{aligned} \widehat{\boldsymbol{\theta}} &=\underset{\boldsymbol{\theta}}{\operatorname{argmin}}\;\mathbb{E}\Vert \boldsymbol{x}-\boldsymbol{f}_{\theta}(\boldsymbol{z})\Vert ^2\\ &=\underset{\boldsymbol{\theta}}{\operatorname{argmin}}\; \mathbb{E}\left\Vert \boldsymbol{f}_{\mathrm{mmse}}(z ; \eta)-\boldsymbol{f}_{\boldsymbol{\theta}}(z)\right\Vert ^{2} \\ &=\underset{\boldsymbol{\theta}}{\operatorname{argmin}}\; \mathbb{E}\Vert \nabla \ln \tilde{p}(z ; \eta)-\frac{1}{\eta}\left(f_{\boldsymbol{\theta}}(z)-z\right)\Vert ^{2}. \end{aligned}\]也就是说, 在去噪算子不是 \(\boldsymbol{f}_{\mathrm{mmse}}\) 时, 我们会首先选择 \(\boldsymbol{\theta}\) 使得 \((f_{\theta}(z)-z)/\eta\) 与 ``score’’ \(\nabla \ln \tilde{p}\) 吻合得最好, 再将至运用于 RED 中.
PnP 与 RED 的一致均衡框架 (Consensus Equilibrium)
为了证明 PnP 的收敛性, 我们直接考虑其迭代格式, 实际上, PnP 可以被视为迭代求解下列不动点方程:
\[\begin{aligned} &\widehat{\boldsymbol{x}}_{\mathrm{pnp}}=\boldsymbol{h}\left(\widehat{\boldsymbol{x}}_{\mathrm{pnp}}-\widehat{\boldsymbol{u}}_{\mathrm{pnp}} ; \eta\right), \\ &\widehat{\boldsymbol{x}}_{\mathrm{pnp}}=\boldsymbol{f}\left(\widehat{\boldsymbol{x}}_{\mathrm{pnp}}+\widehat{\boldsymbol{u}}_{\mathrm{pnp}}\right). \end{aligned}\]其中
\[\begin{aligned} \boldsymbol{h}(\boldsymbol{z} ; \eta) & \triangleq \underset{\boldsymbol{x}\in \mathbb{R}^{n}}{\arg\min}\;\frac{1}{2 \sigma^{2}}\Vert \boldsymbol{y}-\boldsymbol{A} \boldsymbol{x}\Vert ^{2}+\frac{1}{2 \eta}\Vert \boldsymbol{x}-\boldsymbol{z}\Vert ^{2} \\ &=\left(\boldsymbol{A}^{\intercal} \boldsymbol{A}+\frac{\sigma^{2}}{\eta} \boldsymbol{I}\right)^{-1}\left(\boldsymbol{A}^{\intercal} \boldsymbol{y}+\frac{\sigma^{2}}{\eta} \boldsymbol{z}\right) . \end{aligned}\]这个不动点方程可以进一步抽象为
\[\begin{aligned} &\underline{z}=(2 \boldsymbol{G}-\boldsymbol{I})(2 \mathcal{F}-\boldsymbol{I}) \underline{z}, \\ &\underline{z}=\left[\begin{array}{l} z_{1} \\ z_{2} \end{array}\right], \quad \mathcal{F}(\underline{z})=\left[\begin{array}{c} \boldsymbol{h}\left(z_{1} ; \eta\right) \\ \boldsymbol{f}\left(z_{2}\right) \end{array}\right], \quad\mathcal{G}(\underline{z})=\left[\begin{array}{c} \left(z_{1}+z_{2}\right)/2 \\ \left(z_{1}+z_{2}\right)/2 \end{array}\right]. \end{aligned}\]求解这一方程的 Mann 迭代格式 (类似于 Anderson 加速) 为
\[\underline{\boldsymbol{z}}^{(k+1)}=(1-\gamma) \underline{\boldsymbol{z}}^{k}+\gamma(2 \boldsymbol{G}-\boldsymbol{I})(2 \mathcal{F}-\boldsymbol{I}) \underline{\boldsymbol{z}}^{(k)}.\]这就从 Mann 迭代的收敛性即可保证 PnP 的收敛性.
同理, 对于 RED, 若采用 ADMM 求解 (推导与 MAP 的 ADMM 类似, 故省略), 则其迭代写为
\[\begin{aligned} &\widehat{\boldsymbol{x}}_{\mathrm{red}}=\boldsymbol{h}\left(\widehat{\boldsymbol{x}}_{\mathrm{red}}-\widehat{\boldsymbol{u}}_\mathrm{red} ; \eta\right) \\ &\widehat{\boldsymbol{x}}_{\mathrm{red}}=\left(\left(1+\frac{1}{L}\right) \boldsymbol{I}-\frac{1}{L} \boldsymbol{f}\right)^{-1}\left(\widehat{\boldsymbol{x}}_{\mathrm{red}}+\widehat{\boldsymbol{u}}_{\mathrm{red}}\right) \end{aligned}\]更为直观的写法是
\[\begin{aligned} &\widehat{\boldsymbol{x}}_{\mathrm{red}}=\boldsymbol{h}\left(\widehat{\boldsymbol{x}}_{\mathrm{red}}-\widehat{\boldsymbol{u}}_{\mathrm{red}} ; \eta\right) \\ &\widehat{\boldsymbol{x}}_{\mathrm{red}}=\boldsymbol{f}\left(\widehat{\boldsymbol{x}}_{\mathrm{red}}\right)+L \widehat{\boldsymbol{u}}_{\mathrm{red}} \end{aligned}\]用与 PnP 同样的方式也能证明 RED 的收敛性, 这里我们利用上式给出 RED 的另一个解释.
将 \(h\) 代入, 从第一个方程解得
\[\widehat{\boldsymbol{u}}_{\mathrm{red}}=\frac{\eta}{\sigma^{2}} \boldsymbol{A}^{\intercal}\left(\boldsymbol{y}-\boldsymbol{A} \widehat{\boldsymbol{x}}_{\mathrm{red}}\right).\]将之带入第二个方程得
\[\frac{L \eta}{\sigma^{2}} A^{\intercal}\left(A \widehat{\boldsymbol{x}}_{\mathrm{red}}-y\right)=f\left(\widehat{\boldsymbol{x}}_{\mathrm{red}}\right)-\widehat{\boldsymbol{x}}_{\mathrm{red}}\]这实际上是在说, 用来拟合数据误差 (左侧) 必须和去噪的误差 (右侧) 相吻合.
RED via Fixed-point Projection (RED-PRO)
最后, 我们给出 RED 的另一种解释, 也是目前最为完善的理论, 在这一理论下, RED 与 PnP 统一在了一起, 借助比压缩映射更弱的 demicontractive 性质即可证明 PnP 与 RED 的收敛性.
RED-PRO 的问题形式为:
\[\hat{\boldsymbol{x}}_{\mathrm{RED}-\mathrm{PRO}}=\underset{\boldsymbol{x} \in \mathbb{R}^{n}}{\arg \min }\; \ell(\boldsymbol{x} ; \boldsymbol{y}), \quad \text { s.t. } \boldsymbol{x} \in \operatorname{Fix}(\boldsymbol{f}).\]其中 \(\operatorname{Fix}(\boldsymbol{f})\) 表示去噪算子的不动点集合. 上述问题最为直观的解释是: 在所有”好”的图像中寻找与观测最为接近的那个. 之所以这样建模, 是因为由自然图像 (即未加任何噪音) 构成的流形往往是病态且非凸的, 且难以获得有关它的任何信息. 所以, 我们退而求其次, 用 \(\operatorname{Fix}(\boldsymbol{f})\) 来近似自然图像所构成的流形. 从直观上看, 一个完美的去噪算法, 其不动点集就是自然图像所构成的流形. 然而, 主流的去噪算子都离理想状态相去甚远, 上述问题的解高度依赖于去噪算子的选择.
From Demicontractivity to Convergence
Demicontractivity 及其推论
为了论述的严谨性, 我们先给出 \(d\)-demicontractive 映射的定义:
A mapping \(T\) is \(d\)-demicontractive (\(d \in[0,1)\)) if for any \(\boldsymbol{x} \in \mathbb{R}^{n}\) and \(\boldsymbol{z} \in \operatorname{Fix}(T)\) it holds that
\[\Vert T(\boldsymbol{x})-\boldsymbol{z}\Vert ^{2} \leq\Vert \boldsymbol{x}-\boldsymbol{z}\Vert ^{2}+d\Vert T(\boldsymbol{x})-\boldsymbol{x}\Vert ^{2},\]or equivalently
\[\frac{1-d}{2}\Vert \boldsymbol{x}-T(\boldsymbol{x})\Vert ^{2} \leq\langle\boldsymbol{x}-T(\boldsymbol{x}), \boldsymbol{x}-\boldsymbol{z}\rangle.\]
该性质有如下两个重要的推论:
- 假设去噪算子 \(f\) 是 \(d\)-demicontractive 的, 那么可以证明 RED-PRO 实际上是一个凸问题!
- 而当 \(\boldsymbol{f}(0)=0\)时, 则有
RED, RED-PRO 与 PnP 的统一
用以求解 RED-PRO 的混合最速下降法 (Hybrid steepest descent method) 迭代格式为:
\[\begin{aligned} &\boldsymbol{v}_{k+1}=\boldsymbol{x}_{k}-\mu_{k} \nabla \ell\left(\boldsymbol{x}_{k} ; \boldsymbol{y}\right), \\ &\boldsymbol{z}_{k+1}=f\left(\boldsymbol{v}_{k+1}\right), \\ &\boldsymbol{x}_{k+1}=(1-\alpha) \boldsymbol{v}_{k+1}+\alpha \boldsymbol{z}_{k+1}. \end{aligned}\]上述格式具有更为紧凑的迭代形式
\[\boldsymbol{x}_{k+1} = f_{\alpha}(\boldsymbol{x}_{k}-\mu_{k} \nabla \ell(\boldsymbol{x}_{k} ; \boldsymbol{y})),\text{ where } f_{\alpha} = (1-\alpha)\mathrm{Id} + \alpha f.\]这种紧凑的格式与用以求解 MAP 问题的 PnP-PG (Plug-and-Play Proximal Gradient) 类似:
\[\boldsymbol{x}_{k+1}=f\left(\boldsymbol{x}_{k}-\mu_{k} \nabla \ell(\boldsymbol{x} ; y)\right).\]而用以求解 RED 的加速邻近梯度法 (Accelerated Proximal Gradient) 格式为:
\[\begin{aligned} \boldsymbol{v}_{k+1} &=\boldsymbol{x}_{k}-\mu_k \nabla \ell\left(\boldsymbol{x}_{k} ; \boldsymbol{y}\right), \\ \boldsymbol{z}_{k+1} &=\boldsymbol{v}_{k+1}+q_{k}\left(\boldsymbol{v}_{k+1}-\boldsymbol{v}_{k}\right),\text{ (FISTA-like acceleration)} \\ \boldsymbol{x}_{k+1} &=(1-\alpha) \boldsymbol{z}_{k+1}+\alpha f\left(\boldsymbol{z}_{k+1}\right). \text{ (SOR-like acceleration)} \end{aligned}\]因此, 只要令 \(q_k\equiv 0\), 即舍弃类似于 FISTA 的加速步骤, 那么用以求解 RED 的加速邻近梯度法就与用以求解 RED-PRO 的混合最速下降法具有相同的迭代格式, 而当上式中的 \(\alpha\equiv 0\) 时, 即舍弃类似于 SOR 的加速步, 上述格式则与基于用 Proximal Gradient 求解 MAP 的 PnP 格式 (即用 \(f\) 替代 Proximal Gradient 中的 Proximal 步) 相同! 如此我们便用 RED 的加速邻近梯度法统一了三种模型, 并把其他两种当作 RED 的特例, 这样的等价性对收敛性的证明是大有益处的, 这意味着我们只需证明这三者中任意一个的收敛性就可以导出三种算法的收敛性.
收敛性结果
我们直接给出收敛性的结果, 其证明较为复杂, 故略去, 请有兴趣的读者参考原论文: https://epubs.siam.org/doi/abs/10.1137/20M1337168.
Let \(f(\cdot)\) be a continuous \(d\)-demicontractive denoiser and \(\ell(\cdot ; \boldsymbol{y})\) be a proper convex lower semicontinuous differentiable function with \(L\)-Lipschitz gradient \(\nabla \ell(\cdot ; \boldsymbol{y})\). Assume the following:
\[\begin{aligned} (A1)\quad &\alpha \in(0, \frac{1-d}{2}).\\ (A2)\quad &\{\mu_{k}\}_{k \in \mathbb{N}} \subset[0, \infty) \text{ where } \mu_{k} \underset{k \rightarrow \infty}{\rightarrow} 0 \text{ and } \sum_{k \in \mathbb{N}} \mu_{k}=\infty. \end{aligned}\]Then, the sequence \(\{\boldsymbol{x}_{k}\}_{k \in \mathbb{N}}\) generated by
\[\boldsymbol{x}_{k+1} = f_{\alpha}(\boldsymbol{x}_{k}-\mu_{k} \nabla \ell(\boldsymbol{x}_{k} ; \boldsymbol{y})),\text{ where } f_{\alpha} = (1-\alpha)\mathrm{Id} + \alpha f,\]converges to an optimal solution of the RED-PRO problem:
\[\hat{\boldsymbol{x}}_{\mathrm{RED}-\mathrm{PRO}}=\underset{\boldsymbol{x} \in \mathbb{R}^{n}}{\arg \min }\; \ell(\boldsymbol{x} ; \boldsymbol{y}), \quad \text { s.t. } \boldsymbol{x} \in \operatorname{Fix}(f).\]
有了这个结果, 我们便在 Demicontractivity 的条件下证明了三种方法的收敛性!
总结
去噪问题的建模方式多种多样, 它们都有各自的长处和缺点:
- PnP: Inspired by ADMM, Proximal gradient, while lacking objective function.
- RED: Regularization by Denoising, while many denoisers do not satisfy the assumptions.
- RED-PRO: require the denoisers to be demicontractive.
但一旦模型建立好了, 不论采用何种算法 (基于 ADMM 的 PnP 或者基于 Proximal Gradient 的 PnP 或者基于 PDHG 的 PnP), 它们实际上都在求解同一个不动点方程:
\[\boldsymbol{x}_{*} = f_{\alpha}(\boldsymbol{x}_{*}-\mu_{k} \nabla \ell(\boldsymbol{x}_{*} ; \boldsymbol{y})),\text{ where } f_{\alpha} = (1-\alpha)\mathrm{Id} + \alpha f.\]因此, 只要对这个不动点迭代建立收敛性结果即可.
一些可能的方向
- 对于一般的优化问题, 是否也能用 RL 来选择合适的参数?
- 能否将 PnP 收敛性的条件再减弱一点?
- 现有的 PnP 都是针对图像处理或者信号处理设计的, 能否将这种方法推广到一般的含 proximal 算子的算法中去?
本文使用 https://zhuanlan.zhihu.com/p/106057556 创作并发布